
Anjali Phadke's Portfolio
Zombies in Math Class: Algebra 1
Click on the document icon to download a copy of my artifact!
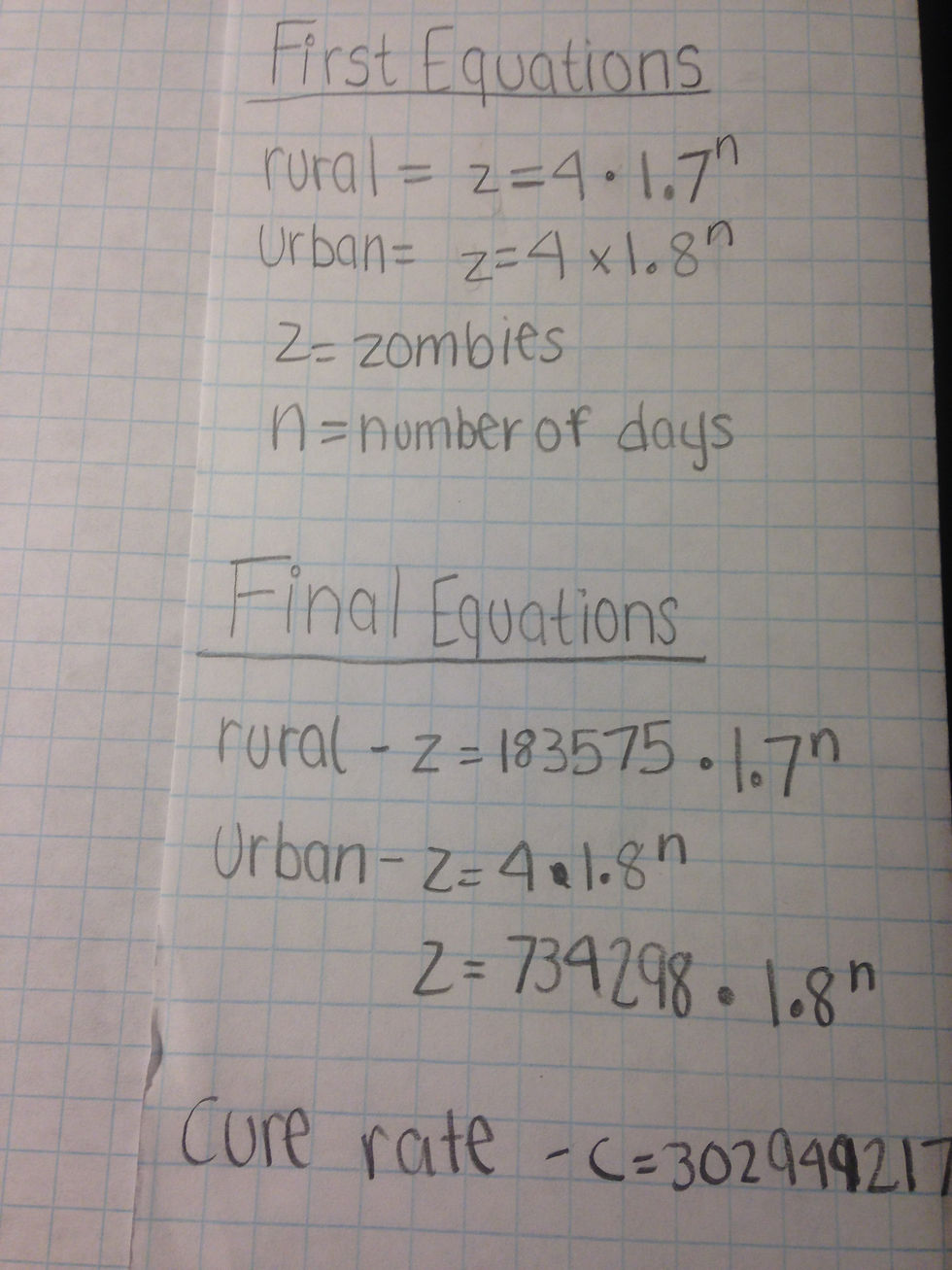
Here is my first artifact. This artifact shows the difference between my first equations vs. my final equations.
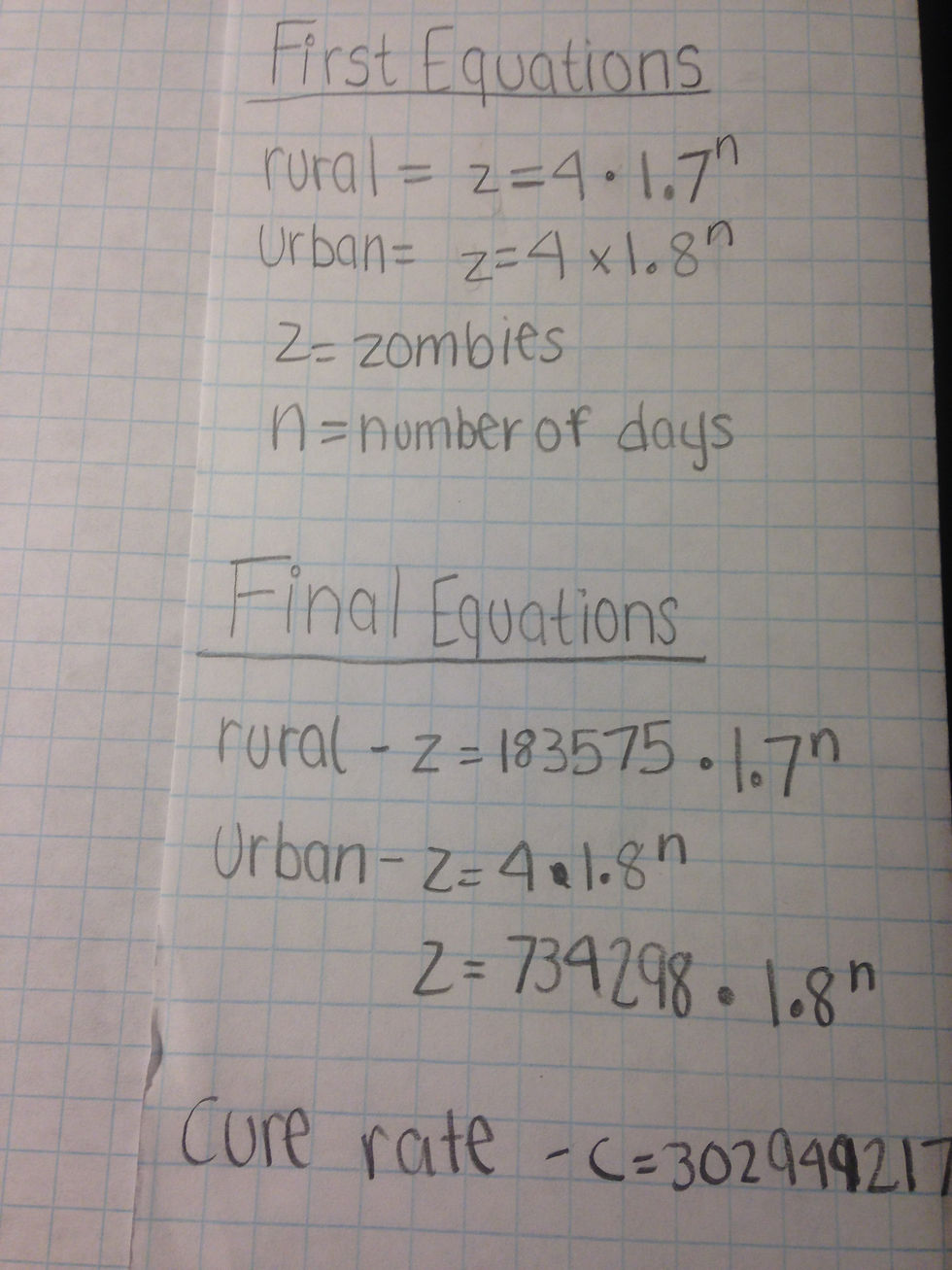
Here is my first artifact. This artifact shows the difference between my first equations vs. my final equations.
At the Dayton Regional STEM School, math and/or math concepts are used every single day. The reason for this might be that we have math class each day, but without math classes, we would use math concepts anyway. Math is one of those subjects that seems completely useless, but in reality, math is necessary to understand in order to function (get it?). Even if we don’t go to school, we use math, sometimes for remedial things such as cooking or drinking (juice of course). Throughout all of this, I am glad to have used math and I am glad that I could put my knowledge about math to good use. I am proud to say that my growth this year has been using my knowledge of math concepts (like exponential functions) to apply towards a real world project.
To me, math has always been work, test, and repeat. We have never used the math concepts we learned to create a new project or collaborative learning assignment that has helped us with more than just math. I feel like we have never really had an assignment where I could actually use another subject to complete the process. In this letter, I didn’t just use math, I used English as well to create the final product of this project. Even though I do use English in every class, the difference between math class and other classes is that we wrote a letter, a really important aspect to learning English. Now that I have been able to use my concepts to apply math in real life, I found another way in which math will be helpful to me in the later years of my life.
This year, I have found another class that I had this same realization in. That class is Chinese. Because I have been learning Chinese, I can use that newfound knowledge to contribute to real world tendencies. What I mean by this is if I possibly needed to translate something in Chinese, I could. If I needed to send an email or a letter in Chinese, I could. The base is basically the same. By this I mean, even though the two subjects are completely different, the way in which they work and function, or the “base” is the same. Now that I have been able to use my math concepts and apply them to real world tendencies, I can use that same knowledge and apply it to other subjects.
One endeavor that supported my growth is the Brain Pox Project. Using math, we were to answer questions given to us by Governor Kasich about the deadly disease, Brain Pox. Not to worry though, this disease is completely unreal. We were given a “fake disease” so that we wouldn’t have to use real data (regarding deaths, percentage infected etc.) found on the internet or other sources. We used mathematical models as well as a letter to give Governor Kasich all the information he needed to see if Ohio would survive the fake deadly disease, Brain Pox. Some main questions during this project included, “When will Ohio become infected?” and “When will the Continental U.S. become infected?” Before we started the actual project, we read an article about the problem of Brain Pox. It included information about Brain Pox including how “The disease causes the person to die and immediately come back to life with loss of limb control, hysteria, insomnia, cannibalism, and mindlessness.” Also, it included information about how Brain Pox is only spread through touch. After we read the article, we read about what we were supposed to do, or the requirements of the project. Then, we were given a brainstorming sheet to include all of ideas (given information, information we need to know, assumptions, how we can use math, and our mathematical models). Then we created an Excel spreadsheet that gave us answers to the questions we had. Basically, we calculated the first few points of the equations we created and let Excel do the rest (we pulled down the corner of a box with an equation or how to calculate the answer and pulled it down so that the rest of the boxes below it would have numbers on them.) After that, we created our letters based on the prior information we got. When we did this, we had a few examples of what the letter should look like. For example, one of the paragraphs in the example letter states that “in another paragraph, you must have solutions. Without solutions, you are only complaining. Offer assistance in solving the problem. Remind the reader where they can contact you. (Here you summarize what is going on (answer the questions) and discuss what actions should be taken.) Finally, we created a presentation that explained the answers to the questions that we had from the beginning. Each group was given a question to answer (one example question being “When will the Continental U.S. become infected with Brain Pox?). After we got our questions, we created PowerPoint presentations that explained the answer to the question using math (tables, graphs, equations, explanations etc.) Then, we presented to a small group of students!
My first artifact is the before and after of the equations we used. It fits into the process because it shows our confusion and understanding of our problem and what we did to fix it. First of all, I am in honors Algebra 1. Because of this, my partner and I’s project was a little tougher than other students’ projects. We used exponential equations in this project. An exponential equation is one in which a variable occurs in the exponent. Exponential functions always have some positive number other than 1 as the base. If the variable 2^x is negative, then that symbolizes exponential decay. If the variable is positive, then that models exponential growth. The general exponential function model is y=b^x. In the equation for this specific project, x was the number of days, y was the number of people and b was the exponential increase or decrease (the percentage of increase). Because of the learning in the artifact, I grew. This was the first step to the project, where I had to use my knowledge of math to apply to real world tendencies.
When my partner and I first started this project, we created our equations. The information given to us about the growth of the disease was that the disease grew by 70% each day in rural areas and 80% each day in urban areas each day. We made the assumption that the disease started with a family of 4. We thought it was simple. We would use 4 as the starting value for both equations and add 1.7 or 1.8 for the exponential growth. Our first equations were y=4*1.7^x (rural) and y=4*1.8^x. But, there was a problem with this. Because the disease started in Columbus, Ohio (which is not a rural area) there was no way that the rural areas could have exponential growth in the disease unless Columbus was fully infected. So, we had 2 equations for urban areas and only 1 equation for rural areas. Our equation for urban areas was the same as before, but the only difference was that the rural area equation didn’t apply anymore. Before we went ahead and started to create the other equations, we had to figure out when Columbus was fully infected with zombies. We found the actual population of Columbus, which was 822,553. Basically, we put in days for x and kept on calculating until we got close to 822553. For the sake of convenience, we made an assumption that the population of Columbus was 917873 people. If we didn’t do this, then we would have to cut into specific hours and minutes and that would’ve been too confusing. After 21 days, Columbus was fully infected so the original urban equation wouldn’t work anymore. At this step, there was a lot of research involved. We looked at some statistics of Ohio and found out that 80 percent of Ohio was of urban area and only 20 percent of Ohio was rural. We made an assumption that 80 percent of the 917873 people would continually be infecting other people in an urban setting and 20 percent of those 917873 people would be infecting others in a rural setting. So, we calculated 20 percent of 917873 and got 183575. We calculated 80 percent of 917873 and got 734298. Our final equations were Rural- z=183575X1.7^n, Urban: z=4X1.8^n, z= 734298X1.8^n, Cure Rate: c=302949217X.8^n. The cure rate was simple. For 10 days only, the number of zombies decreased by 20 percent every day. So, we just put the full population of the Continental U.S. (the whole U.S. would be infected) as the starting value and .8 and the exponential value. By this, I mean that the population of the Continental U.S. would replace “a” in y=a*b^x and .8 would replace b.
My second artifact is my final letter to Governor Kasich (it was an assignment, so the letter wasn’t actually going to him). In this specific assignment, we had a few steps to create the final letter. We first started the draft of the letter by using a template that our teacher had given us. When we wrote this draft, there were some problems. See, applying the knowledge to real world tendencies is the easy part, but putting those words in a letter is harder than it seems. The first paragraph was the introduction. Any letter has to have an introduction. In this paragraph we explained what the problem was (Brain Pox) and how we would explain how to fix the problem. The second paragraph discussed our assumptions and how they were important to completing the problem. The third paragraph showed our equations and discussed why we came up with those particular equations. We introduced our tables and graphs and placed them after or throughout the paragraph. There also could have been an additional paragraph that described what was happening using Math terms and concepts. The last paragraph talked about the solutions to the problem. We also offered Governor Kasich assistance by telling them how to solve the problem. Even though this was a letter, there was a lot of math involved and there was a lot to fix. For example, in the original brain storming sheet we had, there were a few assumptions about math or the problem that we had to write.
There were a few problems with our letter. We had assumptions in a paragraph about equations and vice versa. For example, we explained how Brain Pox started with a family of four in our paragraph about equations. Assumptions were really important to this process for a multitude of reasons. For example, one of our assumptions was that if a person got cured, they couldn’t become infected again. If we didn’t create this assumption beforehand, then our graph, table, equations, and the data would be completely different. If a person could become infected again after becoming cured, then the number of infected people would be drastically higher. In this project, if we didn’t talk about our assumptions or if we didn’t explain the importance, then Governor Kasich could be dealing with a lot more infected people then he thought he would. Because of this, the consequences regarding the fictitious disease could be disastrous. Our graphs’ curves would be showing higher numbers (because it is an exponential graph, the curves would be more defined which means the growth is higher because there are more people). Also, in the letter, if I didn’t explicitly explain my assumptions before I explained the equations, then the reader wouldn’t understand the importance of all the steps I went through to get all the information where it is. What I mean by this is, because the assignment was to write a letter to Governor Kasich, I had to make sure that the letter showed great importance and urgency. If I didn’t list all my assumptions where they were supposed to go, then that takes away some of the professionalism from the letter. This is really how I grew. Even though the letter was English, it was how I applied my math concepts to a real world tendency. In an exponential graph (if there is a y-intercept) then the line will start above the starting value. For example, our y-intercept or starting value for the cure rate equation was the population of the Continental U.S. or 302949217. Negative exponents or starting values that go from 0-1 show exponential decay. This means that the graph trend or line will be completely opposite compared to its positive counterpart. In our specific letter, exponential decay related to the number of infected people. The decay factor for the equation was .8, which means that the number of infected people decreased by 20% each day. We had to use exponential growth for the growth of infected people and we had to use exponential decay for the decay of infected people (the cure). Throughout all of this, I have been able to use my knowledge to apply to real world tendencies.
My first artifact is an example of my growth because it shows how I understood my confusion and fixed it before I could actually apply the concepts. I had to understand the math concepts before I could really apply them to the world. My second artifact is a good example of my growth because it shows how I actually applied the concepts to a letter. I explained the math concepts and all the graphs in my letter and I really grew in actually using math for a real world tendency.
Because I found another way to use math in a real world situation, I can apply this knowledge into other subjects, like physics, so that I can help myself in the future. For example, I could write in Chinese for a future patient or answer phone calls in Chinese. I could use math in my future job as a pediatrician if I wanted to, the implications are endless. I will never be perfect at math. That is a fact. But, now that I have found another way to use math in a real world situation, I am closer to being better at applying concepts to real life. These concepts that I used really helped me in the project that we created. Now, I hope I can use this same concept for the rest of my classes or the rest of my high school career.